algebraic geometry - Locally Closed Immersion - Mathematics Stack Exchange
The Language of Schemes
FOUNDATIONS OF ALGEBRAIC GEOMETRY CLASS 27
Morphism | Jock Club | Ascetic House
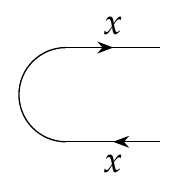
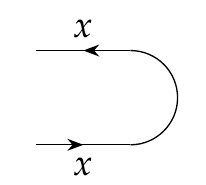
LECTURE 1: NAKAJIMA QUIVER VARIETIES 1. Geometric invariant theory Recall that an algebraic group G is called (linearly) reducti
algebraic geometry - diagonal morphism is a (locally) closed embedding - Mathematics Stack Exchange
Glass Morphism 3d Illustration Closed Sky Stock Vector (Royalty Free) 1928041634 | Shutterstock
The canonical embedding of an unramified morphism in an étale morphism
NvdL 4b4$5
arXiv:0808.3753v1 [math.AG] 27 Aug 2008
POINTS HAVING THE SAME RESIDUE FIELD AS THEIR IMAGE UNDER A MORPHISM 1. Main result Our result, loosely speaking, is that in a n
CLOSED] Derive morphism to/from inital/terminal object from zero morphism · Issue #7 · homalg-project/CAP_project · GitHub
ON THE MORPHISMS AND TRANSFORMATIONS OF 1. Introduction. The closed sets of operations, or clones, on an arbitrary set A, i.e.,
ct.category theory - Multiplication and division by a morphism under the “inner composition” in closed monoidal categories - MathOverflow
arXiv:math/0302005v1 [math.AG] 31 Jan 2003
Regular Languages Closed Under Homomorphism - YouTube
FOUNDATIONS OF ALGEBRAIC GEOMETRY CLASS 18
Lecture 74 - Chapter 4: Compact Closed Categories - Azimuth Forum
Week 8: two classes) (5) A scheme is locally noetherian if there is an affine cover by SpecAi where each Ai is noetherian. A sc
separated
